图论常见结论及例题

风铃夜行2025-07-052025-07-05

图论常见结论及例题

常见结论

要在有向图上求一个最大点集，使得任意两个点之间至少存在一条路径（可以是从到，也可以反过来，这两种有一个就行），即求解最长路；
要求出连通图上的任意一棵生成树，只需要跑一遍 bfs ；
给出一棵树，要求添加尽可能多的边，使得其是二分图：对树进行二分染色，显然，相同颜色的点之间连边不会破坏二分图的性质，故可添加的最多的边数即为；
当一棵树可以被黑白染色时，所有染黑节点的度之和等于所有染白节点的度之和；
在竞赛图中，入度小的点，必定能到达出度小（入度大）的点 See 。
在竞赛图中，将所有点按入度从小到大排序，随后依次遍历，若对于某一点满足前个点的入度之和恰好等于，那么对于上一次满足这一条件的点，到点构成一个新的强连通分量 See 。

举例说明，设满足上方条件的点为，那么点到构成一个强连通分量、点到构成一个强连通分量。
选择图中最少数量的边删除，使得图不连通，即求最小割；如果是删除点，那么拆点后求最小割 See。
如果一张图是平面图，那么其边数一定小于等于 See 。
若一张有向完全图存在环，则一定存在三元环。
竞赛图三元环计数：See 。
有向图判是否存在环直接用 topsort；无向图判是否存在环直接用 dsu，也可以使用 topsort，条件变为 deg[i] <= 1 时入队。

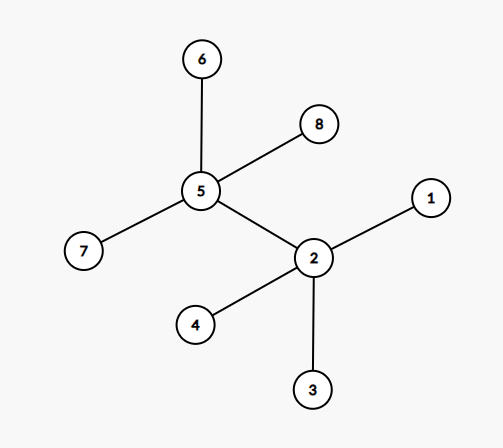
常见例题

杂

题意：给出一棵节点数为的树，要求将点分割为个点对，使得点对的点之间的距离和最大。

可以转化为边上问题：对于每一条边，其被利用的次数即为 $其左边的点的数量其右边的点的数量$ ，使用树形计算一遍即可。如下图样例，答案为。

vector<int> val(n + 1, 1);
int ans = 0;
function<void(int, int)> dfs = [&](int x, int fa) {
    for (auto y : ver[x]) {
        if (y == fa) continue;
        dfs(y, x);
        val[x] += val[y];
        ans += min(val[y], k - val[y]);
    }
};
dfs(1, 0);
cout << ans << endl;

题意：以哪些点为起点可以无限的在有向图上绕

概括一下这些点可以发现，一类是环上的点，另一类是可以到达环的点。建反图跑一遍 topsort 板子，根据容斥，未被移除的点都是答案 See 。

题意：添加最少的边，使得有向图变成一个 SCC

将原图的 SCC 缩点，统计缩点后的新图上入度为和出度为的点的数量 $、$ ，答案即为。过程大致是先将一个出度为的点和一个入度为的点相连，剩下的点随便连 See 。

题意：添加最少的边，使得无向图变成一个 E-DCC

将原图的 E-DCC 缩点，统计缩点后的新图上入度为的点（叶子结点）的数量，答案即为。过程大致是每次找两个叶子结点（但是还有一些条件限制）相连，若最后余下一个点随便连 See 。

题意：在树上找到一个最大的连通块，使得这个联通内点权和边权之和最大，输出这个值，数据中存在负数的情况。

使用 dfs 即可解决。

LL n, point[N];
LL ver[N], head[N], nex[N], tot; bool v[N];
map<pair<LL, LL>, LL> edge;
// void add(LL x, LL y) {}
void dfs(LL x) {
    for (LL i = head[x]; i; i = nex[i]) {
        LL y = ver[i];
        if (v[y]) continue;
        v[y] = true; dfs(y); v[y] = false;
    }
    for (LL i = head[x]; i; i = nex[i]) {
        LL y = ver[i];
        if (v[y]) continue;
        point[x] += max(point[y] + edge[{x, y}], 0LL);
    }
}
void Solve() {
    cin >> n;
    FOR(i, 1, n) cin >> point[i];
    FOR(i, 2, n) {
        LL x, y, w; cin >> x >> y >> w;
        edge[{x, y}] = edge[{y, x}] = w;
        add(x, y), add(y, x);
    }
    v[1] = true; dfs(1); LL ans = -MAX18;
    FOR(i, 1, n) ans = max(ans, point[i]);
    cout << ans << endl;
}

Prüfer 序列：凯莱公式

题意：给定个顶点，可以构建出多少棵标记树？

时的样例如上，通项公式为。

Prüfer 序列

一个个点条边的带标号无向图有个连通块。我们希望添加条边使得整个图连通，求方案数量 See 。

设表示每个连通块的数量，通项公式为，当时答案为。

单源最短/次短路计数

const int N = 2e5 + 7, M = 1e6 + 7;
int n, m, s, e; int d[N][2], v[N][2]; // 0 代表最短路， 1 代表次短路
Z num[N][2];

void Clear() {
    for (int i = 1; i <= n; ++ i) h[i] = edge[i] = 0;
    tot = 0;
    for (int i = 1; i <= n; ++ i) num[i][0] = num[i][1] = v[i][0] = v[i][1] = 0;
    for (int i = 1; i <= n; ++ i) d[i][0] = d[i][1] = INF;
}

int ver[M], ne[M], h[N], edge[M], tot;
void add(int x, int y, int w) {
    ver[++ tot] = y, ne[tot] = h[x], h[x] = tot;
    edge[tot] = w;
}

void dji() {
    priority_queue<PIII, vector<PIII>, greater<PIII> > q; q.push({0, s, 0});
    num[s][0] = 1; d[s][0] = 0;
    while (!q.empty()) {
        auto [dis, x, type] = q.top(); q.pop();
        if (v[x][type]) continue; v[x][type] = 1;
        for (int i = h[x]; i; i = ne[i]) {
            int y = ver[i], w = dis + edge[i];
            if (d[y][0] > w) {
                d[y][1] = d[y][0], num[y][1] = num[y][0];
                    // 如果找到新的最短路，将原有的最短路数据转化为次短路
                q.push({d[y][1], y, 1});
                d[y][0] = w, num[y][0] = num[x][type];
                q.push({d[y][0], y, 0});
            }
            else if (d[y][0] == w) num[y][0] += num[x][type];
            else if (d[y][1] > w) {
                d[y][1] = w, num[y][1] = num[x][type];
                q.push({d[y][1], y, 1});
            }
            else if (d[y][1] == w) num[y][1] += num[x][type];
        }
    }
}
void Solve() {
    cin >> n >> m >> s >> e;
    Clear(); //多组样例务必完全清空
    for (int i = 1; i <= m; ++ i) {
        int x, y, w; cin >> x >> y; w = 1;
        add(x, y, w), add(y, x, w);
    }
    dji();
    Z ans = num[e][0];
    if (d[e][1] == d[e][0] + 1) {
        ans += num[e][1]; // 只有在次短路满足条件时才计算（距离恰好比最短路大1）
    }
    cout << ans.val() << endl;
}

判定图中是否存在负环

使用 SPFA ，复杂度为，其中常数相较裸的 SPFA 更高。

const int N = 1e5 + 7, M = 1e6 + 7;
int n, m;
int ver[M], ne[M], h[N], edge[M], tot;
int d[N], v[N], num[N];

void add(int x, int y, int w)  {
    ver[++ tot] = y, ne[tot] = h[x], h[x] = tot;
    edge[tot] = w;    
}
bool spfa() {
    queue<int> q;
    for (int i = 1; i <= n; ++ i) q.push(i), v[i] = 1; //全部入队
    while(!q.empty()) {
        int x = q.front(); q.pop();
        v[x] = 0;
        for (int i = h[x]; i; i = ne[i]) {
            int y = ver[i];
            if(d[y] > d[x] + edge[i]) {
                num[y] = num[x] + 1;
                if (num[y] >= n) return true;
                d[y] = d[x] + edge[i];
                if(!v[y]) q.push(y), v[y] = 1;
            }
        }
    }
    return false;
}
int main() {
    cin >> n >> m;
    for (int i = 1; i <= m; ++ i) {
        int x, y, w; cin >> x >> y >> w;
        add(x, y, w);
    }
    if(spfa() == true) cout << "Yes" << endl;
    else cout << "No" << endl;
}

输出任意一个三元环

原题：给出一张有向完全图，输出任意一个三元环上的全部元素 See 。使用 dfs，复杂度，可以扩展到非完全图和无向图。

int n;
cin >> n;
vector<vector<int>> a(n + 1, vector<int>(n + 1));
for (int i = 1; i <= n; ++i) {
    for (int j = 1; j <= n; ++j) {
        char x;
        cin >> x;
        if (x == '1') a[i][j] = 1;
    }
}

vector<int> vis(n + 1);
function<void(int, int)> dfs = [&](int x, int fa) {
    vis[x] = 1;
    for (int y = 1; y <= n; ++y) {
        if (a[x][y] == 0) continue;
        if (a[y][fa] == 1) {
            cout << fa << " " << x << " " << y;
            exit(0);
        }
        if (!vis[y]) dfs(y, x); // 这一步的if判断很关键
    }
};
for (int i = 1; i <= n; ++i) {
    if (!vis[i]) dfs(i, -1);
}
cout << -1;

带权最小环大小与计数

原题：给出一张有向带权图，求解图上最小环的长度、有多少个这样的最小环 See 。使用 floyd，复杂度为，可以扩展到无向图。

LL Min = 1e18, ans = 0;
for (int k = 1; k <= n; k++) {
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            if (dis[i][j] > dis[i][k] + dis[k][j]) {
                dis[i][j] = dis[i][k] + dis[k][j];
                cnt[i][j] = cnt[i][k] * cnt[k][j] % mod;
            } else if (dis[i][j] == dis[i][k] + dis[k][j]) {
                cnt[i][j] = (cnt[i][j] + cnt[i][k] * cnt[k][j] % mod) % mod;
            }
        }
    }
    for (int i = 1; i < k; i++) {
        if (a[k][i]) {
            if (a[k][i] + dis[i][k] < Min) {
                Min = a[k][i] + dis[i][k];
                ans = cnt[i][k];
            } else if (a[k][i] + dis[i][k] == Min) {
                ans = (ans + cnt[i][k]) % mod;
            }
        }
    }
}

最小环大小

原题：给出一张无向图，求解图上最小环的长度、有多少个这样的最小环 See 。使用 floyd，可以扩展到有向图。

int flody(int n) {
    for (int i = 1; i <= n; ++ i) {
        for (int j = 1; j <= n; ++ j) {
            val[i][j] = dis[i][j]; // 记录最初的边权值
        }
    }
    int ans = 0x3f3f3f3f;
    for (int k = 1; k <= n; ++ k) {
        for (int i = 1; i < k; ++ i) { // 注意这里是没有等于号的
            for (int j = 1; j < i; ++ j) {
                ans = min(ans, dis[i][j] + val[i][k] + val[k][j]);
            }
        }
    for (int i = 1; i <= n; ++ i) { // 往下是标准的flody
        for (int j = 1; j <= n; ++ j) {
                dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
            }
        }
    }
    return ans;
}

使用 bfs，复杂度为。

auto bfs = [&] (int s) {
    queue<int> q; q.push(s);
    dis[s] = 0;
    fa[s] = -1;
    while (q.size()) {
        auto x = q.front(); q.pop();
        for (auto y : ver[x]) {
            if (y == fa[x]) continue;
            if (dis[y] == -1) {
                dis[y] = dis[x] + 1;
                fa[y] = x;
                q.push(y);
            }
            else ans = min(ans, dis[x] + dis[y] + 1);
        }
    }
};
for (int i = 1; i <= n; ++ i) {
    fill(dis + 1, dis + 1 + n, -1);
    bfs(i);
}
cout << ans;

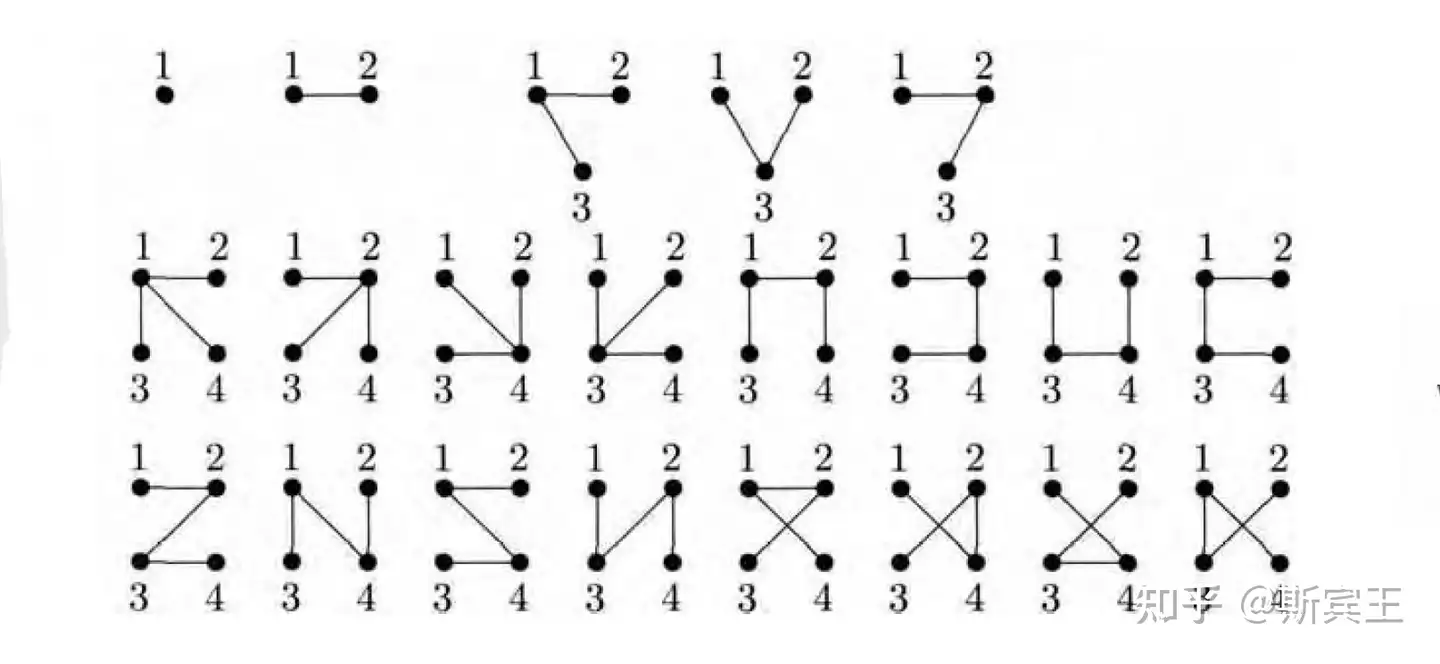
本质不同简单环计数

原题：给出一张无向图，输出简单环的数量 See 。注意这里环套环需要分别多次统计，下图答案应当为。使用状压 dp，复杂度为，可以扩展到有向图。

int n, m;
cin >> n >> m;
vector<vector<int>> G(n);
for (int i = 0; i < m; i++) {
    int u, v;
    cin >> u >> v;
    u--, v--;
    G[u].push_back(v);
    G[v].push_back(u);
}
vector<vector<LL>> dp(1 << n, vector<LL>(n));
for (int i = 0; i < n; i++) dp[1 << i][i] = 1;
LL ans = 0;
for (int st = 1; st < (1 << n); st++) {
    for (int u = 0; u < n; u++) {
        if (!dp[st][u]) continue;
        int start = st & -st;
        for (auto v : G[u]) {
            if ((1 << v) < start) continue;
            if ((1 << v) & st) {
                if ((1 << v) == start) {
                    ans += dp[st][u];
                }
            } else {
                dp[st | (1 << v)][v] += dp[st][u];
            }
        }
    }
}
cout << (ans - m) / 2 << "\n";

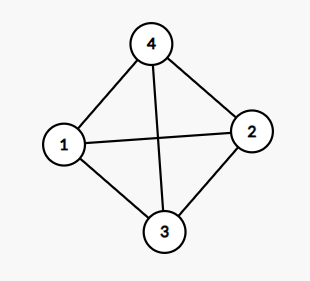
输出任意一个非二元简单环

原题：给出一张无向图，不含自环与重边，输出任意一个简单环的大小以及其上面的全部元素 See 。注意输出的环的大小是随机的，不等价于最小环。

由于不含重边与自环，所以环的大小至少为，使用 dfs 处理出 dfs 序，复杂度为，可以扩展到有向图；如果有向图中二元环也允许计入答案，则需要删除下方标注行。

vector<int> dis(n + 1, -1), fa(n + 1);
auto dfs = [&](auto self, int x) -> void {
    for (auto y : ver[x]) {
        if (y == fa[x]) continue; // 二元环需删去该行
        if (dis[y] == -1) {
            dis[y] = dis[x] + 1;
            fa[y] = x;
            self(self, y);
        } else if (dis[y] < dis[x]) {
            cout << dis[x] - dis[y] + 1 << endl;
            int pre = x;
            cout << pre << " ";
            while (pre != y) {
                pre = fa[pre];
                cout << pre << " ";
            }
            cout << endl;
            exit(0);
        }
    }
};
for (int i = 1; i <= n; i++) {
    if (dis[i] == -1) {
        dis[i] = 0;
        dfs(dfs, 1);
    }
}

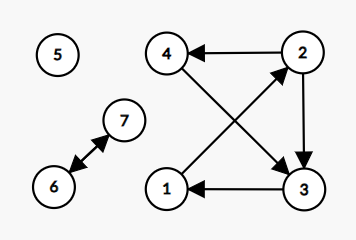
有向图环计数

原题：给出一张有向图，输出环的数量。注意这里环套环仅需要计算一次，数据包括二元环和自环，下图例应当输出个环。使用 dfs 染色法，复杂度为。

int ans = 0;
vector<int> vis(n + 1);
auto dfs = [&](auto self, int x) -> void {
    vis[x] = 1;
    for (auto y : ver[x]) {
        if (vis[y] == 0) {
            self(self, y);
        } else if (vis[y] == 1) {
            ans++;
        }
    }
    vis[x] = 2;
};
for (int i = 1; i <= n; i++) {
    if (!vis[i]) {
        dfs(dfs, i);
    }
}
cout << ans << endl;

输出有向图任意一个环

原题：给出一张有向图，输出任意一个环，数据包括二元环和自环。使用 dfs 染色法。

vector<int> dis(n + 1), vis(n + 1), fa(n + 1);
auto dfs = [&](auto self, int x) -> void {
    vis[x] = 1;
    for (auto y : ver[x]) {
        if (vis[y] == 0) {
            dis[y] = dis[x] + 1;
            fa[y] = x;
            self(self, y);
        } else if (vis[y] == 1) {
            cout << dis[x] - dis[y] + 1 << endl;
            int pre = x;
            cout << pre << " ";
            while (pre != y) {
                pre = fa[pre];
                cout << pre << " ";
            }
            cout << endl;
            exit(0);
        }
    }
    vis[x] = 2;
};
for (int i = 1; i <= n; i++) {
    if (!vis[i]) {
        dfs(dfs, i);
    }
}

判定带环图是否是平面图

原题：给定一个环以一些额外边，对于每一条额外边判定其位于环外还是环内，使得任意两条无重合顶点的额外边都不相交（即这张图构成平面图）See1, See2 。

使用 2-sat。考虑全部边都位于环内，那么“一条边完全包含另一条边”、“两条边完全没有交集”这两种情况都不会相交，可以直接跳过这两种情况的讨论。

signed main() {
    int n, m;
    cin >> n >> m;
    vector<pair<int, int>> in(m);
    for (int i = 0, x, y; i < m; i++) {
        cin >> x >> y;
        in[i] = minmax(x, y);
    }
    TwoSat sat(m);
    for (int i = 0; i < m; i++) {
        auto [s, e] = in[i];
        for (int j = i + 1; j < m; j++) {
            auto [S, E] = in[j];
            if (s < S && S < e && e < E || S < s && s < E && E < e) {
                sat.add(i, 0, j, 0);
                sat.add(i, 1, j, 1);
            }
        }
    }
    if (!sat.work()) {
        cout << "Impossible\n";
        return 0;
    }
    auto ans = sat.answer();
    for (auto it : ans) {
        cout << (it ? "out" : "in") << " ";
    }
}

/END/