三维几何及常见例题

风铃夜行2025-07-052025-07-05

三维几何及常见例题

三维几何必要初始化

点线面封装

struct Point3 {
    ld x, y, z;
    Point3(ld x_ = 0, ld y_ = 0, ld z_ = 0) : x(x_), y(y_), z(z_) {}
    Point3 &operator+=(Point3 p) & {
        return x += p.x, y += p.y, z += p.z, *this;
    }
    Point3 &operator-=(Point3 p) & {
        return x -= p.x, y -= p.y, z -= p.z, *this;
    }
    Point3 &operator*=(Point3 p) & {
        return x *= p.x, y *= p.y, z *= p.z, *this;
    }
    Point3 &operator*=(ld t) & {
        return x *= t, y *= t, z *= t, *this;
    }
    Point3 &operator/=(ld t) & {
        return x /= t, y /= t, z /= t, *this;
    }
    friend Point3 operator+(Point3 a, Point3 b) { return a += b; }
    friend Point3 operator-(Point3 a, Point3 b) { return a -= b; }
    friend Point3 operator*(Point3 a, Point3 b) { return a *= b; }
    friend Point3 operator*(Point3 a, ld b) { return a *= b; }
    friend Point3 operator*(ld a, Point3 b) { return b *= a; }
    friend Point3 operator/(Point3 a, ld b) { return a /= b; }
    friend auto &operator>>(istream &is, Point3 &p) {
        return is >> p.x >> p.y >> p.z;
    }
    friend auto &operator<<(ostream &os, Point3 p) {
        return os << "(" << p.x << ", " << p.y << ", " << p.z << ")";
    }
};
struct Line3 {
    Point3 a, b;
};
struct Plane {
    Point3 u, v, w;
};

其他函数

ld len(P3 p) { // 原点到当前点的距离计算
    return sqrt(p.x * p.x + p.y * p.y + p.z * p.z);
}
P3 crossEx(P3 a, P3 b) { // 叉乘
    P3 ans;
    ans.x = a.y * b.z - a.z * b.y;
    ans.y = a.z * b.x - a.x * b.z;
    ans.z = a.x * b.y - a.y * b.x;
    return ans;
}
ld cross(P3 a, P3 b) {
    return len(crossEx(a, b));
}
ld dot(P3 a, P3 b) { // 点乘
    return a.x * b.x + a.y * b.y + a.z * b.z;
}
P3 getVec(Plane s) { // 获取平面法向量
    return crossEx(s.u - s.v, s.v - s.w);
}
ld dis(P3 a, P3 b) { // 三维欧几里得距离公式
    ld val = (a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y) + (a.z - b.z) * (a.z - b.z);
    return sqrt(val);
}
P3 standardize(P3 vec) { // 将三维向量转换为单位向量
    return vec / len(vec);
}

三维点线面相关

空间三点是否共线

其中第二个函数是专门用来判断给定的三个点能否构成平面的，因为不共线的三点才能构成平面。

bool onLine(P3 p1, P3 p2, P3 p3) { // 三点是否共线
    return sign(cross(p1 - p2, p3 - p2)) == 0;
}
bool onLine(Plane s) {
    return onLine(s.u, s.v, s.w);
}

四点是否共面

bool onPlane(P3 p1, P3 p2, P3 p3, P3 p4) { // 四点是否共面
    ld val = dot(getVec({p1, p2, p3}), p4 - p1);
    return sign(val) == 0;
}

空间点是否在线段上

bool pointOnSegment(P3 p, L3 l) {
    return sign(cross(p - l.a, p - l.b)) == 0 && min(l.a.x, l.b.x) <= p.x &&
           p.x <= max(l.a.x, l.b.x) && min(l.a.y, l.b.y) <= p.y && p.y <= max(l.a.y, l.b.y) &&
           min(l.a.z, l.b.z) <= p.z && p.z <= max(l.a.z, l.b.z);
}
bool pointOnSegmentEx(P3 p, L3 l) { // pointOnSegment去除端点版
    return sign(cross(p - l.a, p - l.b)) == 0 && min(l.a.x, l.b.x) < p.x &&
           p.x < max(l.a.x, l.b.x) && min(l.a.y, l.b.y) < p.y && p.y < max(l.a.y, l.b.y) &&
           min(l.a.z, l.b.z) < p.z && p.z < max(l.a.z, l.b.z);
}

空间两点是否在线段同侧

当给定的两点与线段不共面、点在线段上时返回。

bool pointOnSegmentSide(P3 p1, P3 p2, L3 l) {
    if (!onPlane(p1, p2, l.a, l.b)) { // 特判不共面
        return 0;
    }
    ld val = dot(crossEx(l.a - l.b, p1 - l.b), crossEx(l.a - l.b, p2 - l.b));
    return sign(val) == 1;
}

两点是否在平面同侧

点在平面上时返回。

bool pointOnPlaneSide(P3 p1, P3 p2, Plane s) {
    ld val = dot(getVec(s), p1 - s.u) * dot(getVec(s), p2 - s.u);
    return sign(val) == 1;
}

空间两直线是否平行/垂直

bool lineParallel(L3 l1, L3 l2) {
    return sign(cross(l1.a - l1.b, l2.a - l2.b)) == 0;
}
bool lineVertical(L3 l1, L3 l2) {
    return sign(dot(l1.a - l1.b, l2.a - l2.b)) == 0;
}

两平面是否平行/垂直

bool planeParallel(Plane s1, Plane s2) {
    ld val = cross(getVec(s1), getVec(s2));
    return sign(val) == 0;
}
bool planeVertical(Plane s1, Plane s2) {
    ld val = dot(getVec(s1), getVec(s2));
    return sign(val) == 0;
}

空间两直线是否是同一条

1
2
3

bool same(L3 l1, L3 l2) {
    return lineParallel(l1, l2) && lineParallel({l1.a, l2.b}, {l1.b, l2.a});
}

两平面是否是同一个

bool same(Plane s1, Plane s2) {
    return onPlane(s1.u, s2.u, s2.v, s2.w) && onPlane(s1.v, s2.u, s2.v, s2.w) &&
           onPlane(s1.w, s2.u, s2.v, s2.w);
}

直线是否与平面平行

bool linePlaneParallel(L3 l, Plane s) {
    ld val = dot(l.a - l.b, getVec(s));
    return sign(val) == 0;
}

空间两线段是否相交

bool segmentIntersection(L3 l1, L3 l2) { // 重叠、相交于端点均视为相交
    if (!onPlane(l1.a, l1.b, l2.a, l2.b)) { // 特判不共面
        return 0;
    }
    if (!onLine(l1.a, l1.b, l2.a) || !onLine(l1.a, l1.b, l2.b)) {
        return !pointOnSegmentSide(l1.a, l1.b, l2) && !pointOnSegmentSide(l2.a, l2.b, l1);
    }
    return pointOnSegment(l1.a, l2) || pointOnSegment(l1.b, l2) || pointOnSegment(l2.a, l1) ||
           pointOnSegment(l2.b, l2);
}
bool segmentIntersection1(L3 l1, L3 l2) { // 重叠、相交于端点不视为相交
    return onPlane(l1.a, l1.b, l2.a, l2.b) && !pointOnSegmentSide(l1.a, l1.b, l2) &&
           !pointOnSegmentSide(l2.a, l2.b, l1);
}

空间两直线是否相交及交点

当两直线不共面、两直线平行时返回。

pair<bool, P3> lineIntersection(L3 l1, L3 l2) {
    if (!onPlane(l1.a, l1.b, l2.a, l2.b) || lineParallel(l1, l2)) {
        return {0, {}};
    }
    auto [s1, e1] = l1;
    auto [s2, e2] = l2;
    ld val = 0;
    if (!onPlane(l1.a, l1.b, {0, 0, 0}, {0, 0, 1})) {
        val = ((s1.x - s2.x) * (s2.y - e2.y) - (s1.y - s2.y) * (s2.x - e2.x)) /
              ((s1.x - e1.x) * (s2.y - e2.y) - (s1.y - e1.y) * (s2.x - e2.x));
    } else if (!onPlane(l1.a, l1.b, {0, 0, 0}, {0, 1, 0})) {
        val = ((s1.x - s2.x) * (s2.z - e2.z) - (s1.z - s2.z) * (s2.x - e2.x)) /
              ((s1.x - e1.x) * (s2.z - e2.z) - (s1.z - e1.z) * (s2.x - e2.x));
    } else {
        val = ((s1.y - s2.y) * (s2.z - e2.z) - (s1.z - s2.z) * (s2.y - e2.y)) /
              ((s1.y - e1.y) * (s2.z - e2.z) - (s1.z - e1.z) * (s2.y - e2.y));
    }
    return {1, s1 + (e1 - s1) * val};
}

直线与平面是否相交及交点

当直线与平面平行、给定的点构不成平面时返回。

pair<bool, P3> linePlaneCross(L3 l, Plane s) {
    if (linePlaneParallel(l, s)) {
        return {0, {}};
    }
    P3 vec = getVec(s);
    P3 U = vec * (s.u - l.a), V = vec * (l.b - l.a);
    ld val = (U.x + U.y + U.z) / (V.x + V.y + V.z);
    return {1, l.a + (l.b - l.a) * val};
}

两平面是否相交及交线

当两平面平行、两平面为同一个时返回。

pair<bool, L3> planeIntersection(Plane s1, Plane s2) {
    if (planeParallel(s1, s2) || same(s1, s2)) {
        return {0, {}};
    }
    P3 U = linePlaneParallel({s2.u, s2.v}, s1) ? linePlaneCross({s2.v, s2.w}, s1).second
                                               : linePlaneCross({s2.u, s2.v}, s1).second;
    P3 V = linePlaneParallel({s2.w, s2.u}, s1) ? linePlaneCross({s2.v, s2.w}, s1).second
                                               : linePlaneCross({s2.w, s2.u}, s1).second;
    return {1, {U, V}};
}

点到直线的最近点与最近距离

pair<ld, P3> pointToLine(P3 p, L3 l) {
    ld val = cross(p - l.a, l.a - l.b) / dis(l.a, l.b); // 面积除以底边长
    ld val1 = dot(p - l.a, l.a - l.b) / dis(l.a, l.b);
    return {val, l.a + val1 * standardize(l.a - l.b)};
}

点到平面的最近点与最近距离

pair<ld, P3> pointToPlane(P3 p, Plane s) {
    P3 vec = getVec(s);
    ld val = dot(vec, p - s.u);
    val = abs(val) / len(vec); // 面积除以底边长
    return {val, p - val * standardize(vec)};
}

空间两直线的最近距离与最近点对

tuple<ld, P3, P3> lineToLine(L3 l1, L3 l2) {
    P3 vec = crossEx(l1.a - l1.b, l2.a - l2.b); // 计算同时垂直于两直线的向量
    ld val = abs(dot(l1.a - l2.a, vec)) / len(vec);
    P3 U = l1.b - l1.a, V = l2.b - l2.a;
    vec = crossEx(U, V);
    ld p = dot(vec, vec);
    ld t1 = dot(crossEx(l2.a - l1.a, V), vec) / p;
    ld t2 = dot(crossEx(l2.a - l1.a, U), vec) / p;
    return {val, l1.a + (l1.b - l1.a) * t1, l2.a + (l2.b - l2.a) * t2};
}

三维角度与弧度

空间两直线夹角的 cos 值

任意位置的空间两直线。

1
2
3

ld lineCos(L3 l1, L3 l2) {
    return dot(l1.a - l1.b, l2.a - l2.b) / len(l1.a - l1.b) / len(l2.a - l2.b);
}

空间两平面夹角的 cos 值

ld planeCos(Plane s1, Plane s2) {
    P3 U = getVec(s1), V = getVec(s2);
    return dot(U, V) / len(U) / len(V);
}

直线与平面夹角的 sin 值

ld linePlaneSin(L3 l, Plane s) {
    P3 vec = getVec(s);
    return dot(l.a - l.b, vec) / len(l.a - l.b) / len(vec);
}

空间多边形

正N棱锥体积公式

棱锥通用体积公式，当其恰好是棱长为的正棱锥时，有公式。

1
2
3

ld V(ld l, int n) { // 正n棱锥体积公式
    return l * l * l * n / (12 * tan(PI / n)) * sqrt(1 - 1 / (4 * sin(PI / n) * sin(PI / n)));
}

四面体体积

1
2
3

ld V(P3 a, P3 b, P3 c, P3 d) {
    return abs(dot(d - a, crossEx(b - a, c - a))) / 6;
}

点是否在空间三角形上

点位于边界上时返回。

bool pointOnTriangle(P3 p, P3 p1, P3 p2, P3 p3) {
    return pointOnSegmentSide(p, p1, {p2, p3}) && pointOnSegmentSide(p, p2, {p1, p3}) &&
           pointOnSegmentSide(p, p3, {p1, p2});
}

线段是否与空间三角形相交及交点

只有交点在空间三角形内部时才视作相交。

pair<bool, P3> segmentOnTriangle(P3 l, P3 r, P3 p1, P3 p2, P3 p3) {
    P3 x = crossEx(p2 - p1, p3 - p1);
    if (sign(dot(x, r - l)) == 0) {
        return {0, {}};
    }
    ld t = dot(x, p1 - l) / dot(x, r - l);
    if (t < 0 || t - 1 > 0) { // 不在线段上
        return {0, {}};
    }
    bool type = pointOnTriangle(l + (r - l) * t, p1, p2, p3);
    if (type) {
        return {1, l + (r - l) * t};
    } else {
        return {0, {}};
    }
}

空间三角形是否相交

相交线段在空间三角形内部时才视作相交。

bool triangleIntersection(vector<P3> a, vector<P3> b) {
    for (int i = 0; i < 3; i++) {
        if (segmentOnTriangle(b[i], b[(i + 1) % 3], a[0], a[1], a[2]).first) {
            return 1;
        }
        if (segmentOnTriangle(a[i], a[(i + 1) % 3], b[0], b[1], b[2]).first) {
            return 1;
        }
    }
    return 0;
}

常用结论

平面几何结论归档

hypot 函数可以直接计算直角三角形的斜边长；
边心距是指正多边形的外接圆圆心到正多边形某一边的距离，边长为的正角形的边心距公式为，外接圆半径为的正角形的边心距公式为；
三角形外接圆半径为，其中为三角形面积，内切圆半径为；
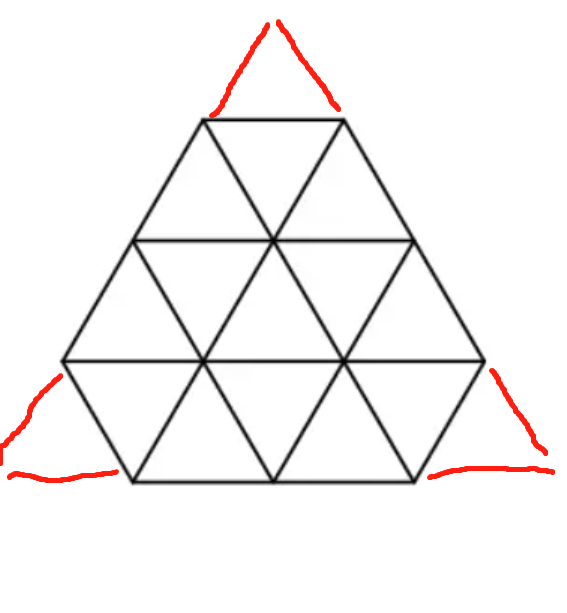
由小正三角形拼成的大正三角形，耗费的小三角形数量即为构成一条边的小三角形数量的平方。如下图，总数量即为 See。
正边形圆心角为，圆周角为。定义正边形上的三个顶点和（可以不相邻），使得，当时，可以取到间的任何一个整数 See。
某一点到直线的距离公式为，等价于。
atan(y / x) 函数仅用于计算第一、四象限的值，而 atan2(y, x) 则允许计算所有四个象限的正反切，在使用这个函数时，需要尽量保证和的类型为整数型，如果使用浮点数，实测会慢十倍。
在平面上有奇数个点以及一个点，构造使得关于对称、构造使得关于对称、……、构造使得关于对称。那么周期为，即与共点、与共点 See 。
已知和两点及这两点的坐标，构造使得关于对称，那么的坐标为。
海伦公式：已知三角形三边长和，定义，则，在使用时需要注意越界问题，本质是铅锤定理，一般多使用叉乘计算三角形面积而不使用该公式。
棱台体积，其中为上下底面积。
正棱台侧面积，其中为上下底周长，为斜高（上下底对应的平行边的距离）。
球面积，体积。
正三角形面积，正四面体面积。
设扇形对应的圆心角弧度为，则面积为。

立体几何结论归档

已知向量，则该向量的三个方向余弦为。其中，。

常用例题

将平面某点旋转任意角度

题意：给定平面上一点，输出将其逆时针旋转度之后的坐标。

signed main() {
    int a, b, d;
    cin >> a >> b >> d;
    
    ld l = hypot(a, b); // 库函数，求直角三角形的斜边
    ld alpha = atan2(b, a) + toArc(d);
    
    cout << l * cos(alpha) << " " << l * sin(alpha) << endl;
}

平面最近点对（set解）

借助 set ，在严格复杂度内求解，比常见的分治法稍快。

template<class T> T sqr(T x) {
    return x * x;
}

using V = Point<int>;
signed main() {
    int n;
    cin >> n;

    vector<V> in(n);
    for (auto &it : in) {
        cin >> it;
    }

    int dis = disEx(in[0], in[1]); // 设定阈值
    sort(in.begin(), in.end());

    set<V> S;
    for (int i = 0, h = 0; i < n; i++) {
        V now = {in[i].y, in[i].x};
        while (dis && dis <= sqr(in[i].x - in[h].x)) { // 删除超过阈值的点
            S.erase({in[h].y, in[h].x});
            h++;
        }
        auto it = S.lower_bound(now);
        for (auto k = it; k != S.end() && sqr(k->x - now.x) < dis; k++) {
            dis = min(dis, disEx(*k, now));
        }
        if (it != S.begin()) {
            for (auto k = prev(it); sqr(k->x - now.x) < dis; k--) {
                dis = min(dis, disEx(*k, now));
                if (k == S.begin()) break;
            }
        }
        S.insert(now);
    }
    cout << sqrt(dis) << endl;
}

平面若干点能构成的最大四边形的面积（简单版，暴力枚举）

题意：平面上存在若干个点，保证没有两点重合、没有三点共线，你需要从中选出四个点，使得它们构成的四边形面积是最大的，注意这里能组成的四边形可以不是凸四边形。

暴力枚举其中一条对角线后枚举剩余两个点，。

signed main() {
    int n;
    cin >> n;
    vector<Pi> in(n);
    for (auto &it : in) {
        cin >> it;
    }
    ld ans = 0;
    for (int i = 0; i < n; i++) {
        for (int j = i + 1; j < n; j++) { // 枚举对角线
            ld l = 0, r = 0;
            for (int k = 0; k < n; k++) { // 枚举第三点
                if (k == i || k == j) continue;
                if (pointOnLineLeft(in[k], {in[i], in[j]})) {
                    l = max(l, triangleS(in[k], in[j], in[i]));
                } else {
                    r = max(r, triangleS(in[k], in[j], in[i]));
                }
            }
            if (l * r != 0) { // 确保构成的是四边形
                ans = max(ans, l + r);
            }
        }
    }
    cout << ans << endl;
}

平面若干点能构成的最大四边形的面积（困难版，分类讨论+旋转卡壳）

题意：平面上存在若干个点，可能存在多点重合、共线的情况，你需要从中选出四个点，使得它们构成的四边形面积是最大的，注意这里能组成的四边形可以不是凸四边形、可以是退化的四边形。

当凸包大小时，说明是退化的四边形，答案直接为；大小恰好为时，说明是凹四边形，我们枚举不在凸包上的那一点，将两个三角形面积相减既可得到答案；大小恰好为时，说明是凸四边形，使用旋转卡壳求解。

using V = Point<int>;
signed main() {
    int Task = 1;
    for (cin >> Task; Task; Task--) {
        int n;
        cin >> n;
        
        vector<V> in_(n);
        for (auto &it : in_) {
            cin >> it;
        }
        auto in = staticConvexHull(in_, 0);
        n = in.size();
        
        int ans = 0;
        if (n > 3) {
            ans = rotatingCalipers(in);
        } else if (n == 3) {
            int area = triangleAreaEx(in[0], in[1], in[2]);
            for (auto it : in_) {
                if (it == in[0] || it == in[1] || it == in[2]) continue;
                int Min = min({triangleAreaEx(it, in[0], in[1]), triangleAreaEx(it, in[0], in[2]), triangleAreaEx(it, in[1], in[2])});
                ans = max(ans, area - Min);
            }
        }
        
        cout << ans / 2;
        if (ans % 2) {
            cout << ".5";
        }
        cout << endl;
    }
}

线段将多边形切割为几个部分

题意：给定平面上一线段与一个任意多边形，求解线段将多边形切割为几个部分；保证线段的端点不在多边形内、多边形边上，多边形顶点不位于线段上，多边形的边不与线段重叠；多边形端点按逆时针顺序给出。下方的几个样例均合法，答案均为。

当线段切割多边形时，本质是与多边形的边交于两个点、或者说是与多边形的两条边相交，设交点数目为，那么答案即为。于是，我们只需要计算交点数量即可，先判断某一条边是否与线段相交，再判断边的两个端点是否位于线段两侧。

signed main() {
    Pi s, e;
    cin >> s >> e; // 读入线段
    
    int n;
    cin >> n;
    vector<Pi> in(n);
    for (auto &it : in) {
        cin >> it; // 读入多边形端点
    }
    
    int cnt = 0;
    for (int i = 0; i < n; i++) {
        Pi x = in[i], y = in[(i + 1) % n];
        cnt += (pointNotOnLineSide(x, y, {s, e}) && segmentIntersection(Line{x, y}, {s, e}));
    }
    cout << cnt / 2 + 1 << endl;
}

平面若干点能否构成凸包（暴力枚举）

题意：给定平面上若干个点，判断其是否构成凸包 See 。

可以直接使用凸包模板，但是代码较长；在这里我们使用暴力枚举试点，也能以的复杂度通过。当两个向量的叉乘时说明其夹角大于等于，使用这一点即可判定。

signed main() {
    int n;
    cin >> n;
    
    vector<Point<ld>> in(n);
    for (auto &it : in) {
        cin >> it;
    }
    
    for (int i = 0; i < n; i++) {
        auto A = in[(i - 1 + n) % n];
        auto B = in[i];
        auto C = in[(i + 1) % n];
        if (cross(A - B, C - B) > 0) {
            cout << "No\n";
            return 0;
        }
    }
    cout << "Yes\n";
}

凸包上的点能构成的最大三角形（暴力枚举）

可以直接使用凸包模板，但是代码较长；在这里我们使用暴力枚举试点，也能以的复杂度通过。

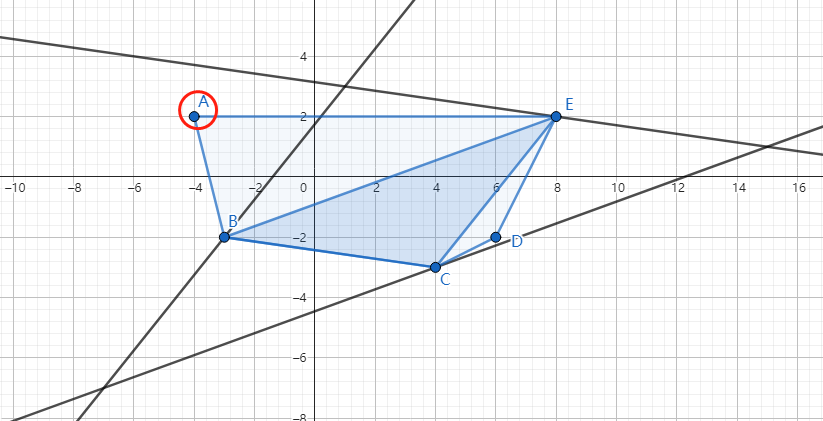
另外补充一点性质：所求三角形的反互补三角形一定包含了凸包上的所有点（可以在边界）。通俗的说，构成的三角形是这个反互补三角形的中点三角形。如下图所示，点不在的反互补三角形内部，故不是最大三角形；才是。

signed main() {
    int n;
    cin >> n;
     
    vector<Point<int>> in(n);
    for (auto &it : in) {
        cin >> it;
    }
    
    #define S(x, y, z) triangleAreaEx(in[x], in[y], in[z])
     
    int i = 0, j = 1, k = 2;
    while (true) {
        int val = S(i, j, k);
        if (S((i + 1) % n, j, k) > val) {
            i = (i + 1) % n;
        } else if (S((i - 1 + n) % n, j, k) > val) {
            i = (i - 1 + n) % n;
        } else if (S(i, (j + 1) % n, k) > val) {
            j = (j + 1) % n;
        } else if (S(i, (j - 1 + n) % n, k) > val) {
            j = (j - 1 + n) % n;
        } else if (S(i, j, (k + 1) % n) > val) {
            k = (k + 1) % n;
        } else if (S(i, j, (k - 1 + n) % n) > val) {
            k = (k - 1 + n) % n;
        } else {
            break;
        }
    }
    cout << i + 1 << " " << j + 1 << " " << k + 1 << endl;
}

凸包上的点能构成的最大四角形的面积（旋转卡壳）

由于是凸包上的点，所以保证了四边形一定是凸四边形，时间复杂度。

template<class T> T rotatingCalipers(vector<Point<T>> &p) {
    #define S(x, y, z) triangleAreaEx(p[x], p[y], p[z])
    int n = p.size();
    T ans = 0;
    auto nxt = [&](int i) -> int {
        return i == n - 1 ? 0 : i + 1;
    };
    for (int i = 0; i < n; i++) {
        int p1 = nxt(i), p2 = nxt(nxt(nxt(i)));
        for (int j = nxt(nxt(i)); nxt(j) != i; j = nxt(j)) {
            while (nxt(p1) != j && S(i, j, nxt(p1)) > S(i, j, p1)) {
                p1 = nxt(p1);
            }
            if (p2 == j) {
                p2 = nxt(p2);
            }
            while (nxt(p2) != i && S(i, j, nxt(p2)) > S(i, j, p2)) {
                p2 = nxt(p2);
            }
            ans = max(ans, S(i, j, p1) + S(i, j, p2));
        }
    }
    return ans;
    #undef S
}

判断一个凸包是否完全在另一个凸包内

题意：给定一个凸多边形和一个凸多边形，询问是否被包含，分别判断严格/不严格包含。例题。

考虑严格包含，使用点集计算出凸包，使用两个点集计算出不严格凸包，如果包含，那么应该与完全相等；考虑不严格包含，在计算凸包时严格即可。最终以复杂度求解，且代码不算很长。

/END/